導(dǎo)言
光作為一種重要的信息載體和能量形式,其特性與行為的研究一直是光學(xué)領(lǐng)域的核心內(nèi)容。渦旋光是一種具有獨特螺旋相位結(jié)構(gòu)和軌道角動量的特殊光束,與傳統(tǒng)的平面波或高斯光束不同,其波前呈現(xiàn)螺旋狀,相位分布圍繞光束中心具有2π的整數(shù)倍變化,這使得每個光子攜帶了與拓?fù)潆姾蓴?shù)相關(guān)的軌道角動量。這種獨特的性質(zhì)賦予了渦旋光在眾多領(lǐng)域(光通信、光學(xué)成像、光學(xué)操縱、量子光學(xué)、激光加工、光存儲等領(lǐng)域)潛在的應(yīng)用價值。研究渦旋光的衍射特性,不僅有助于深入理解渦旋光的基本物理性質(zhì),揭示其在傳播過程中的行為規(guī)律,還能為上述應(yīng)用提供堅實的理論基礎(chǔ),推動相關(guān)技術(shù)的發(fā)展和創(chuàng)新。通過對渦旋光衍射的研究,可以優(yōu)化渦旋光的產(chǎn)生、傳輸和檢測方法,提高其在實際應(yīng)用中的性能和效率,從而為解決實際問題提供更有效的光學(xué)工具和技術(shù)方案。
摘要
本文就基于衍射圖樣的拓?fù)潆姾蓴?shù)測量方法進(jìn)行了理論分析、數(shù)值模擬和實驗驗證。在理論分析方面,基于惠更斯-菲涅爾原理和標(biāo)量衍射理論,建立渦旋光衍射的數(shù)學(xué)模型,推導(dǎo)渦旋光在不同衍射條件下的光場分布表達(dá)式,結(jié)合數(shù)值模擬,利用 MATLAB軟件平臺,編寫相應(yīng)的程序?qū)u旋光衍射過程進(jìn)行模擬仿真。通過數(shù)值模擬,可以直觀地展示渦旋光在不同參數(shù)條件下的衍射光場分布情況,深入分析各種因素對衍射特性的影響,為實驗研究提供指導(dǎo)和補(bǔ)充。在實驗研究方面,搭建渦旋光產(chǎn)生與衍射實驗平臺,利用空間光調(diào)制器、螺旋相位板等光學(xué)元件產(chǎn)生不同拓?fù)潆姾蓴?shù)的渦旋光,并通過設(shè)置不同的衍射障礙物或孔徑,觀察和記錄渦旋光的衍射圖樣。采用 CCD 相機(jī)、光電探測器等設(shè)備對衍射光場進(jìn)行測量和分析,獲取實驗數(shù)據(jù),驗證理論分析和數(shù)值仿真的正確性。
渦旋光衍射理論分析
基于惠更斯 - 菲涅爾原理和標(biāo)量衍射理論,可對渦旋光的衍射特性進(jìn)行深入的理論分析。假設(shè)渦旋光的初始電場分布為[數(shù)學(xué)公式],在柱坐標(biāo)系下,其表達(dá)式可寫為:
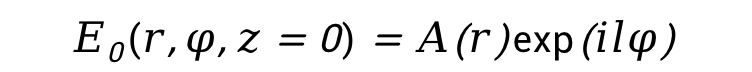
其中, 是振幅函數(shù),描述了渦旋光在徑向的振幅分布,l為拓?fù)浜蓴?shù),
是振幅函數(shù),描述了渦旋光在徑向的振幅分布,l為拓?fù)浜蓴?shù), 是方位角。
是方位角。
當(dāng)渦旋光遇到衍射障礙物或通過衍射孔徑時,根據(jù)惠更斯 - 菲涅爾原理,波面上的每一點都可看作是新的子波源,這些子波源發(fā)出的子波在空間中相互干涉、疊加,從而形成衍射光場。對于菲涅爾衍射,在距離衍射屏z處的光場分布 可通過菲涅爾衍射積分公式計算:
可通過菲涅爾衍射積分公式計算:
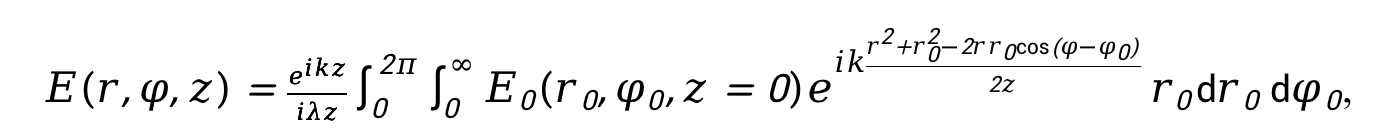
其中, 為波數(shù),
為波數(shù), 是光的波長,
是光的波長, 是衍射屏上的坐標(biāo),
是衍射屏上的坐標(biāo), 是觀察平面上的坐標(biāo)。
是觀察平面上的坐標(biāo)。
在夫瑯禾費衍射條件下,當(dāng)接收屏和衍射屏的距離足夠遠(yuǎn)時,衍射光場的分布可通過夫瑯和費衍射衍射積分公式簡化計算:
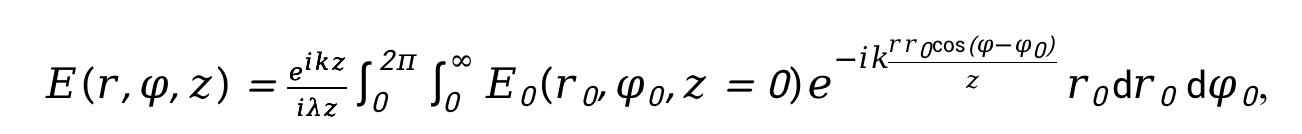
在衍射過程中,渦旋光的相位和強(qiáng)度會發(fā)生顯著變化。由于渦旋光本身具有螺旋相位結(jié)構(gòu) ,在衍射時,這種相位結(jié)構(gòu)會與衍射引起的相位變化相互作用。對于相位變化,衍射會導(dǎo)致相位的重新分布,使得渦旋光的螺旋相位在空間中的分布發(fā)生改變,從而影響其波前的形狀和傳播方向。而在強(qiáng)度方面,衍射會使渦旋光的光強(qiáng)分布發(fā)生變化,原本的環(huán)形光強(qiáng)分布在衍射后可能會出現(xiàn)旁瓣、暗紋等復(fù)雜結(jié)構(gòu),光強(qiáng)的最大值和最小值的位置也會發(fā)生改變。通過對上述衍射積分公式的分析和計算,可以深入了解渦旋光在衍射過程中相位和強(qiáng)度的具體變化規(guī)律,為進(jìn)一步研究渦旋光的衍射特性提供理論基礎(chǔ)。
,在衍射時,這種相位結(jié)構(gòu)會與衍射引起的相位變化相互作用。對于相位變化,衍射會導(dǎo)致相位的重新分布,使得渦旋光的螺旋相位在空間中的分布發(fā)生改變,從而影響其波前的形狀和傳播方向。而在強(qiáng)度方面,衍射會使渦旋光的光強(qiáng)分布發(fā)生變化,原本的環(huán)形光強(qiáng)分布在衍射后可能會出現(xiàn)旁瓣、暗紋等復(fù)雜結(jié)構(gòu),光強(qiáng)的最大值和最小值的位置也會發(fā)生改變。通過對上述衍射積分公式的分析和計算,可以深入了解渦旋光在衍射過程中相位和強(qiáng)度的具體變化規(guī)律,為進(jìn)一步研究渦旋光的衍射特性提供理論基礎(chǔ)。
渦旋光經(jīng)過不同光闌的衍射計算模型
假設(shè)渦旋光經(jīng)過一個特殊形狀的光闌(三角形、星形、方形、太極形等),光闌放置在處為初始光場平面,假設(shè)光闌可用數(shù)學(xué)形式 表示,則此時渦旋光經(jīng)過此光闌后在觀察面z處的光場分布可以用衍射積分公式進(jìn)行計算:
表示,則此時渦旋光經(jīng)過此光闌后在觀察面z處的光場分布可以用衍射積分公式進(jìn)行計算:
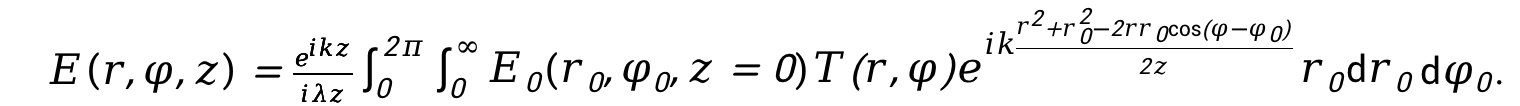
衍射孔徑的形狀對渦旋光的衍射圖樣有著顯著影響。不同形狀的衍射孔徑會導(dǎo)致不同的衍射圖樣特征。
數(shù)值仿真理論基礎(chǔ)
理論上可以用衍射積分公式進(jìn)行直接積分或者進(jìn)行直接的數(shù)值計算,但是在實際數(shù)值仿真計算中,我們可以將衍射積分公式進(jìn)行改寫,其在直角坐標(biāo)系下可以寫為
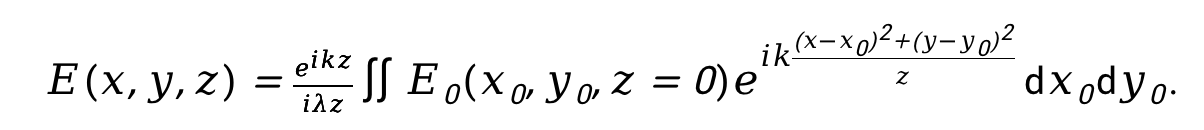
將上式中積分內(nèi)的指數(shù)項展開,得
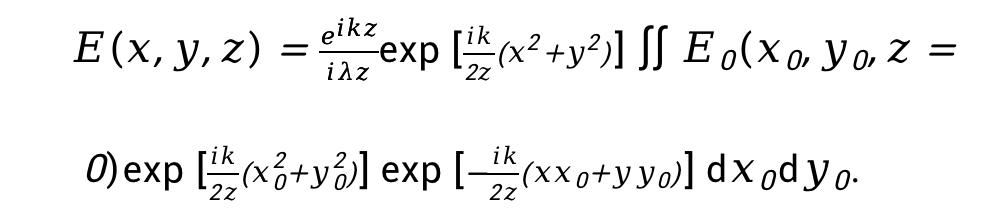
定義脈沖響應(yīng):
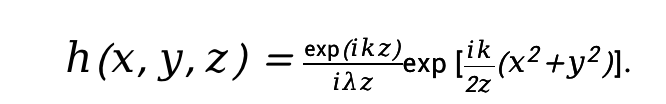
令初始光場為 ,則觀察面z處的光場復(fù)振幅分布為
,則觀察面z處的光場復(fù)振幅分布為
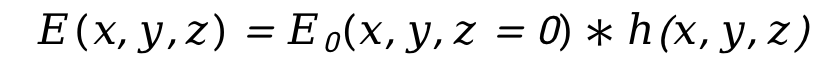
式中,* 表示卷積。由卷積定理可得
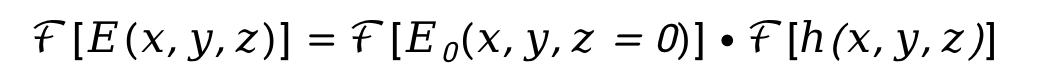
對脈沖響應(yīng)進(jìn)行傅里葉變換,得到菲涅爾傳遞函數(shù) 如下
如下
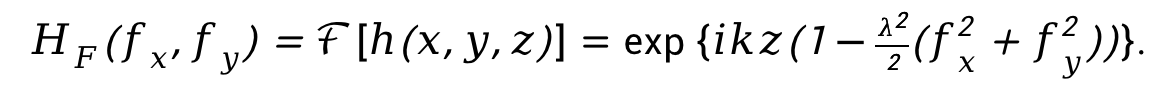
因此,觀察面z處的光場可改寫為
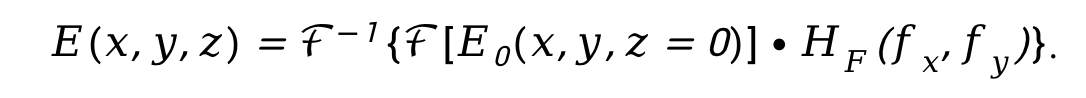
由此得到了新的衍射計算形式,通過計算初始平面光場的頻譜,而后乘以傳遞函數(shù)得到觀察面的頻譜,最后進(jìn)行傅里葉逆變換得到觀察面的光場。而上述計算形式結(jié)合MATLAB軟件平臺中的fft2和ifft2函數(shù)可以非常快速的進(jìn)行數(shù)值仿真計算。
渦旋光束經(jīng)過不同光闌后的數(shù)值仿真結(jié)果
利用寫好的MATLAB代碼我們仿真了四種異形光闌,其形狀分別為正三角形、星形、方形和太極形,其示意圖如下圖1所示。

圖1:四種異形光闌示意圖。
利用MATLAB得到高斯渦旋光束,然后將其經(jīng)過利用不同分布函數(shù)產(chǎn)生相應(yīng)的異形光闌,利用衍射數(shù)值計算算法,得到渦旋光束經(jīng)過不同光闌后在觀察平面的光強(qiáng)分布圖。

圖2:渦旋光經(jīng)過不同光闌后的衍射圖樣。實際對應(yīng)的物理尺寸為1cm*1cm。
如圖2,下面一行分別示意等邊三角形、五角星、矩形和太極孔光闌。上面一行則是渦旋光經(jīng)過光闌后對應(yīng)的衍射圖案。值得注意的是,三角孔衍射的結(jié)果能夠被應(yīng)用于渦旋光的檢測,不僅可以檢測出渦旋光的拓?fù)浜桑⑶移涑蜻€可以很方便地得到渦旋光拓?fù)浜傻恼?fù)。
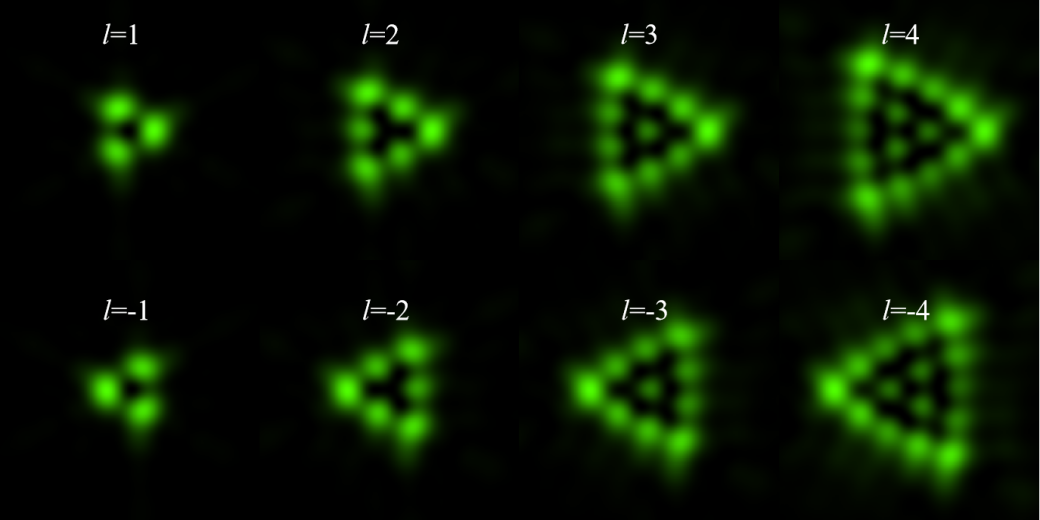
圖3:不同拓?fù)浜蓽u旋光經(jīng)過三角形光闌后的衍射圖樣。
如圖3所示,當(dāng)渦旋光經(jīng)過三角形光闌衍射后,一條邊上的散斑數(shù)目恰好等于拓?fù)浜蓴?shù)加1,并且三角形衍射圖樣的朝向與拓?fù)浜傻恼?fù)負(fù)號有關(guān)。同樣的我們可以分別計算出渦旋光經(jīng)過星形光闌、方形光闌以及太極光闌之后的衍射圖樣,分別如圖4、圖5、圖6所示。

圖4:不同拓?fù)浜蓽u旋光經(jīng)過星形光闌后的衍射圖樣。

圖5:不同拓?fù)浜蓽u旋光經(jīng)過方形光闌后的衍射圖樣。

圖6:不同拓?fù)浜蓽u旋光經(jīng)過太極光闌后的衍射圖樣。
可以看到,渦旋光束經(jīng)過不同的異形光闌后其衍射圖樣都各不相同,其衍射圖樣也能與拓?fù)浜蓴?shù)及其符號相關(guān)聯(lián),具體的對應(yīng)規(guī)律沒有如三角形光闌的明顯,但是通過圖像視覺的方法可以得到對應(yīng)的關(guān)系。
我們利用衍射計算程序可以計算出在不同平面的衍射圖樣,從而揭示出這些衍射圖樣的形成過程,圖7演示的是渦旋光經(jīng)過三角形光闌后的衍射圖樣的形成過程。

圖7:渦旋光經(jīng)過三角形光闌后的孔衍射圖樣的演化過程
改變衍射屏的形狀,我們同樣可以模擬其他形狀孔徑的衍射圖樣。圖8展示了渦旋光經(jīng)過星形光闌衍射圖樣的形成過程。

圖8:渦旋光經(jīng)過星形光闌后的孔衍射圖樣的演化過程
繼續(xù)改變衍射屏的形狀,可以模擬渦旋光經(jīng)過方形光闌的衍射圖樣,圖9展示了渦旋光經(jīng)過方形孔徑衍射圖樣的形成過程。
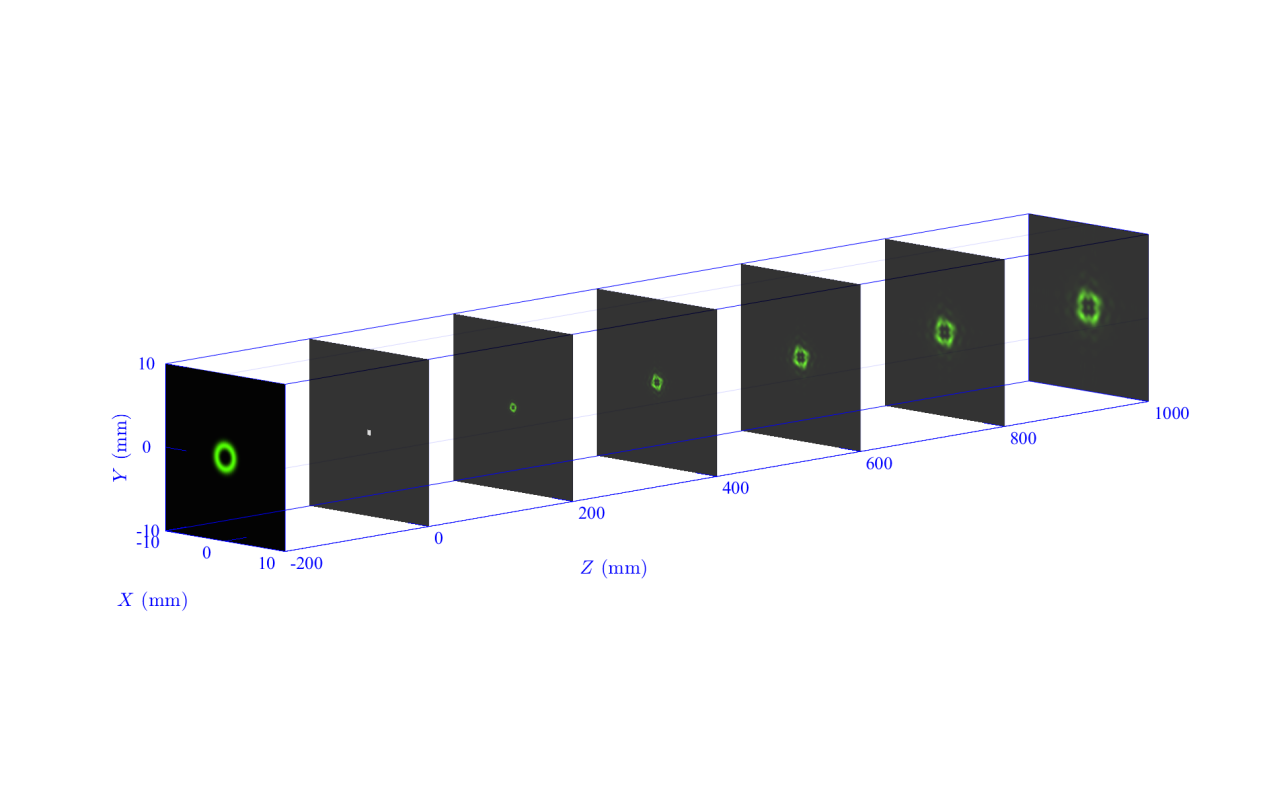
圖9:渦旋光經(jīng)過方形光闌后的孔衍射圖樣的形成過程
同樣的,圖10展示了渦旋光經(jīng)過太極光闌孔徑衍射圖樣的演化過程。

圖10:渦旋光經(jīng)過太極光闌后的孔衍射圖樣的演化過程
渦旋光束經(jīng)過不同光闌后的實驗實現(xiàn)和結(jié)果展示
上面展示的都是理論仿真得到的數(shù)據(jù),那么在實驗中真實的情況又是如何呢?我們將結(jié)合UPOLabs的液晶空間光調(diào)制器HDSLM80R Plus來開展實驗驗證。
由于HDSLM80R Plus是相位型空間光調(diào)制器(SLM),首先我們需要設(shè)法利用相位型器件實現(xiàn)振幅型器件的等效方法,閃耀光柵法是一種十分有效的方案,通過將異形光闌數(shù)學(xué)表達(dá)式與閃耀光柵進(jìn)行相乘操作,可以很容易地實現(xiàn)相位型器件轉(zhuǎn)換為振幅型器件使用。同時我們將渦旋相位也結(jié)合在其中,這樣渦旋光的產(chǎn)生就不需要引入額外的調(diào)制器件。實驗光路示意圖如圖11所示。具體操作后加載到SLM的圖片如圖12-圖15所示。
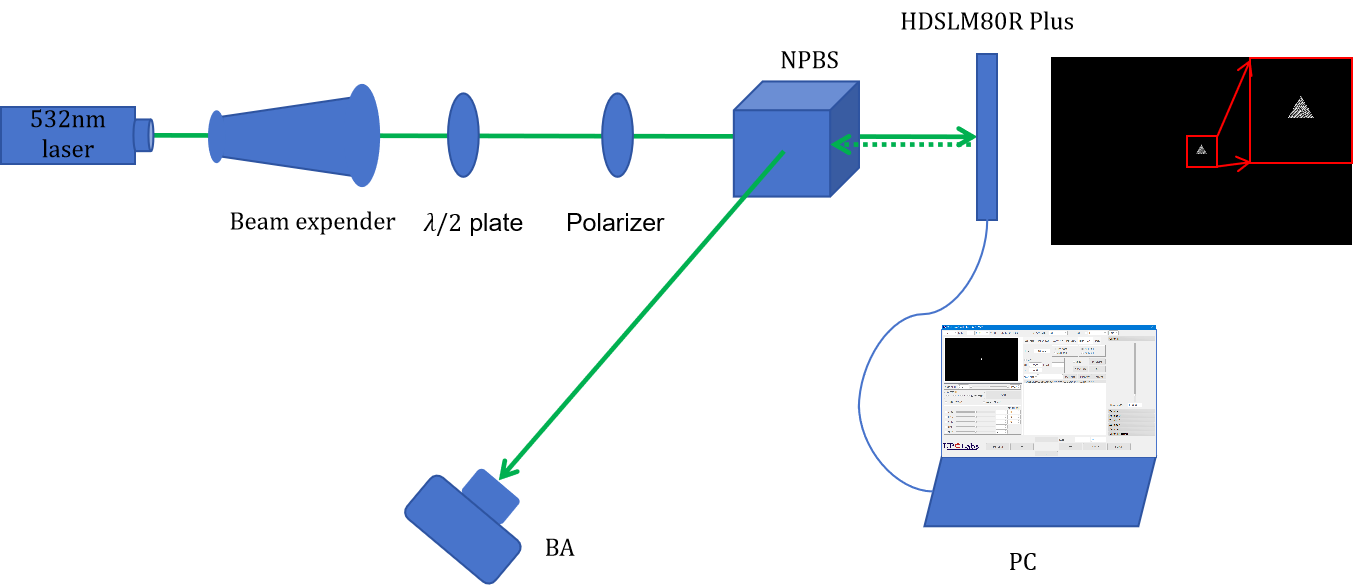
圖11 實驗光路示意圖。BA:光斑分析儀;PC:筆記本電腦。

圖12:渦旋光三角形光闌衍射SLM加載圖像示意圖
(渦旋光拓?fù)浜蔀?的圖例)
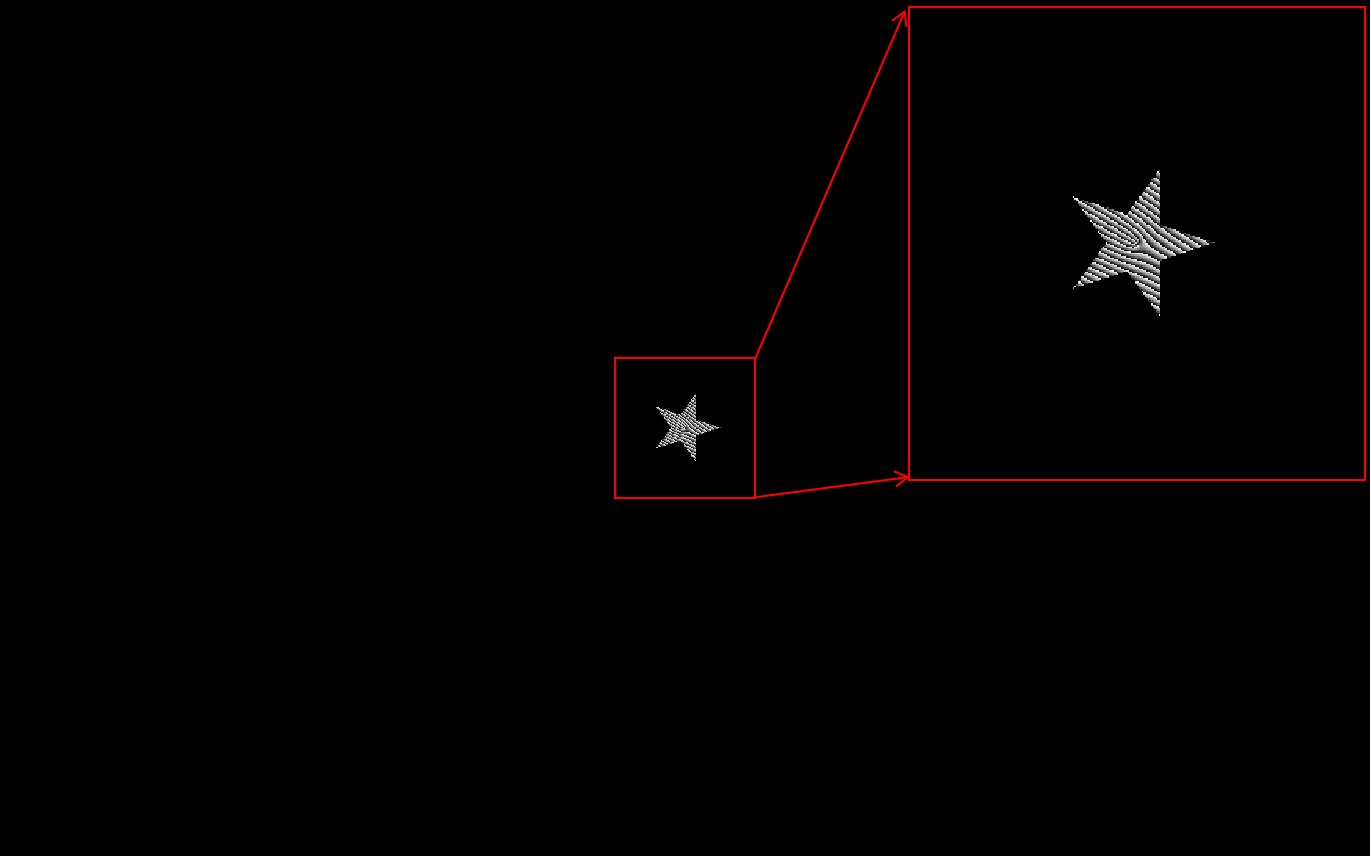
圖13:渦旋光星形光闌衍射SLM加載圖像示意圖
(渦旋光拓?fù)浜蔀?的圖例)

圖14:渦旋光方形光闌衍射SLM加載圖像示意圖
(渦旋光拓?fù)浜蔀?的圖例)
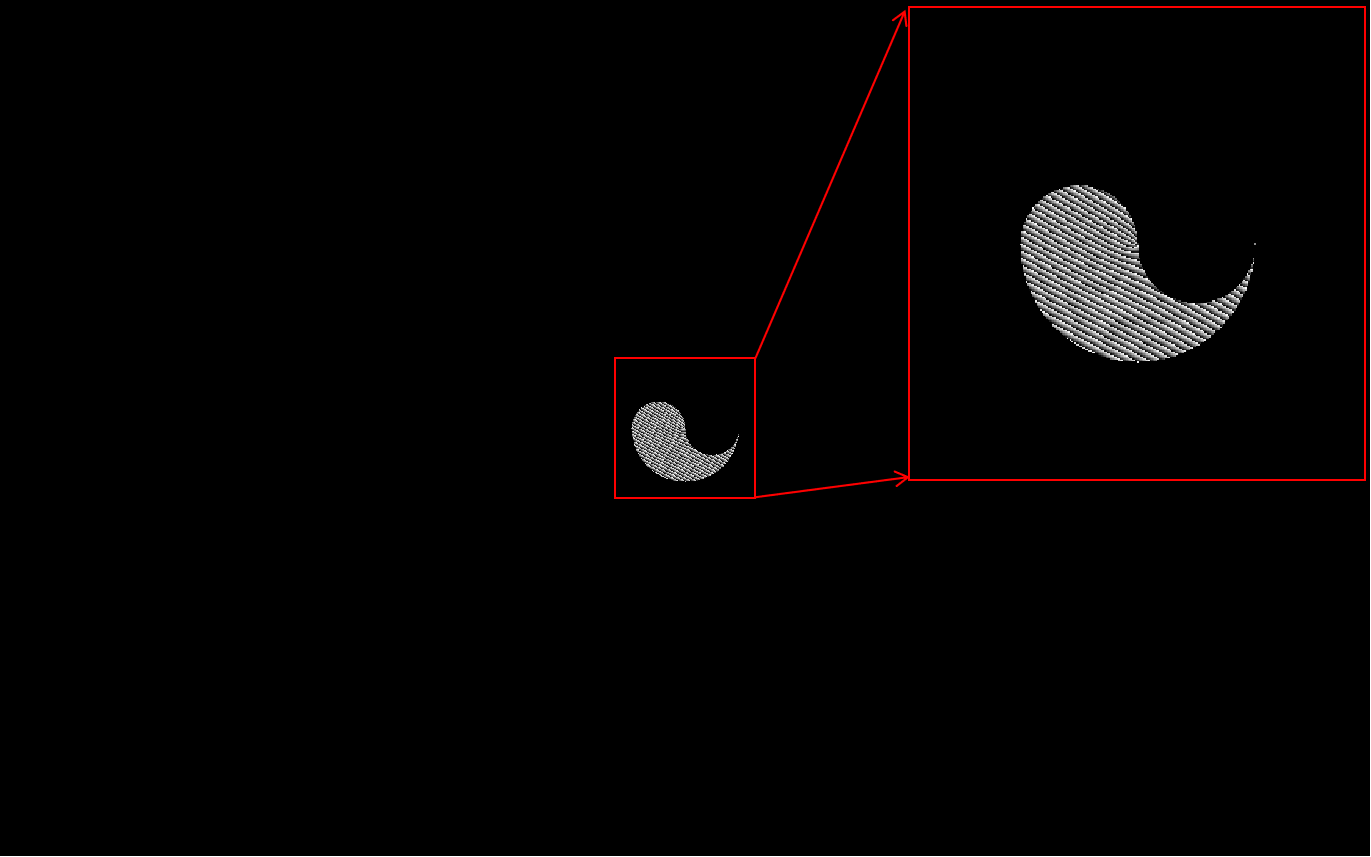
圖15:渦旋太極形光闌衍射SLM加載圖像示意圖
(渦旋光拓?fù)浜蔀?的圖例)
具體的衍射實驗結(jié)果如圖16-圖19所示,圖中的實際物理尺寸均為1cm*1cm。可以發(fā)現(xiàn)實驗結(jié)果通理論仿真結(jié)果十分吻合。這表明理論仿真結(jié)合SLM實驗研究渦旋光束的衍射特性是一套切實可行的研究方法,相信該研究范式在其他光場傳輸研究中也能發(fā)揮其效果。

圖16:不同拓?fù)浜蓽u旋光經(jīng)過三角形光闌后的衍射圖樣實驗結(jié)果。
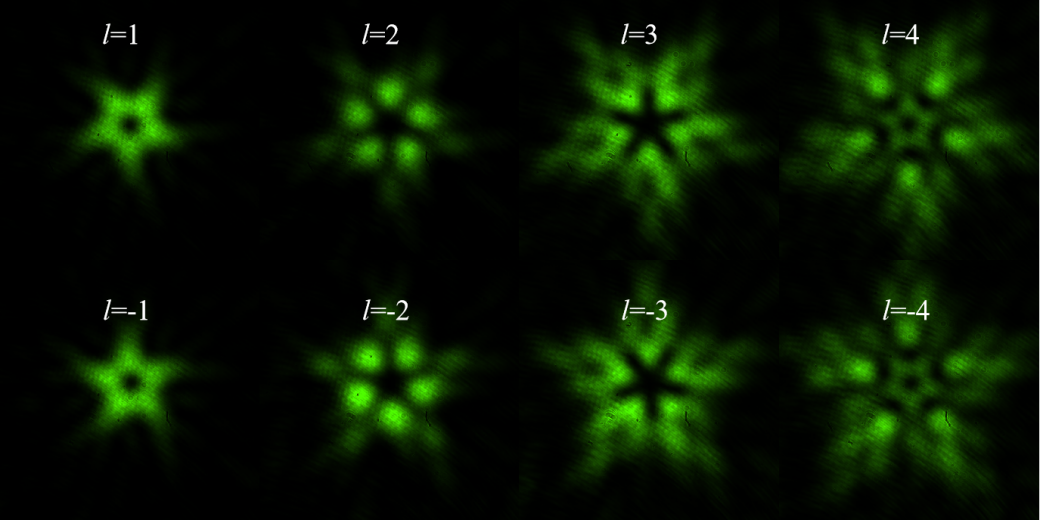
圖17:不同拓?fù)浜蓽u旋光經(jīng)過星形光闌后的衍射圖樣實驗結(jié)果。

圖18:不同拓?fù)浜蓽u旋光經(jīng)過方形光闌后的衍射圖樣實驗結(jié)果。
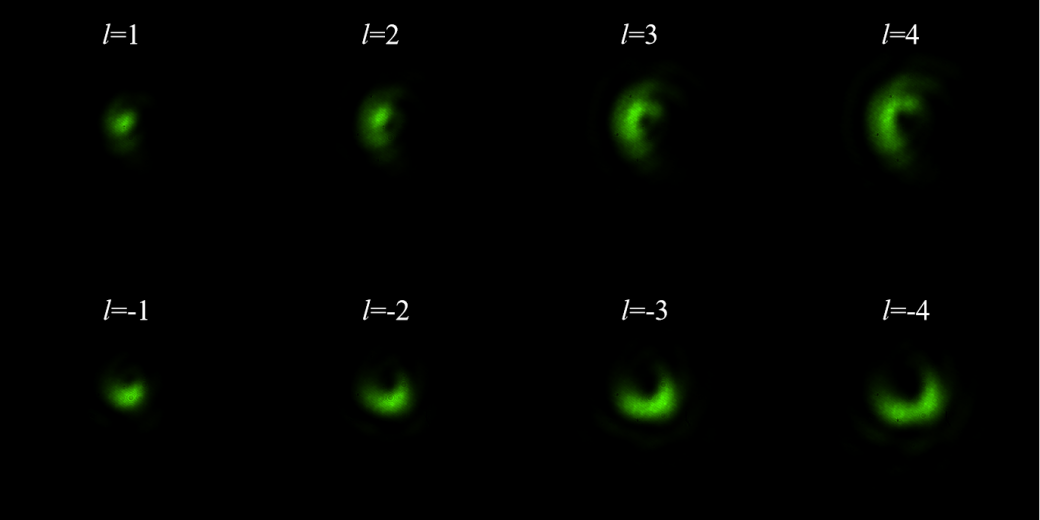
圖19:不同拓?fù)浜蓽u旋光經(jīng)過太極光闌后的衍射圖樣。
參考文獻(xiàn)
[1] 1. W. Goodman, Introduction to Fourier Optics. New York, NY, USA:McGraw-Hill2005.
[2] C. Rosales-Guzmán and A. Forbes, How to Shape Light With Spatial Light.Modulators. Bellingham, WA, USA: SPIE,2017.
[3] Shen D, Wang K, Zhao D. Generation and propagation of a new kind of power-exponent-phase vortex beam[J]. Optics express, 2019, 27(17): 24642-24653.